Antonio Augusto Gorni

Companhia Siderúrgica Paulista - COSIPA, Brazil

- INTRODUCTION

From the beginning of digital computing to the end of the 1980's, virtually all data processing applications adopted a basic approach: programmed computation. This approach requires the previous development of a mathematical or logical algorithm to solve the problem at hand, which have to be subsequentely translated into any computational language¹.

This approach is limited, because it only can be used in cases where the processing to be made can be precisely described in a known rule set. However, sometimes the development of such rule set is hard or impossible. Besides that, as computers work in a totally logical form, the final software must to be practically perfect to work correctly. So, the development of computer software is, indeed, a succession of "project-test-interactive improvement" cycles that can demand much time, effort and money.

During the late 1980's a revolutionary approach for data and information processing appeared: neural networks. This technique does not require previous development of algorithms or rule sets to analyse data. This can minimize significantly the software development work needed for a given application. In most cases, the neural network is previously submitted to a "training" step using real known data, extracting then the methodology necessary to perform the required data processing. That is, a neural network is able to extract the required relationships from real data, avoiding the previous development of any model. This is the approach intuitively used in the biological neural systems, particularly by human beings.

- A TUTORIAL

One can understand more easily the difference between the behavior of programmed computation and neural networks comparing computers and humans. For example, a computer can perform mathematical operations more quickly and precisely than an human. However, the human can recognize faces and complex images in a more precise, efficient and quick way than the best computer available². One of the reasons for this performance difference can be attributed to the distinct organization forms of computers and biological neural systems. A computer generally consists of a processor working alone, executing instructions delivered by a programmer, one-by-one. Biological neural systems, by its turn, consist of billions of nervous cells - that is, neurons - with an high degree of interconnection between themselves.

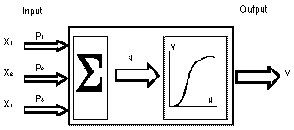
Neurons can perform simple calculations without the need to be previously programmed^1-5. The basic element of a neural network is called, naturally, neuron. It is also known as node, processing element or perceptron. A neuron is schematically showed in Figure 1. The links between neurons are called synapses. The input signal to a given neuron is calculated as follows. The outputs of the preceding neurons of the network are multiplicated by their respective synapse weights. These results are summed up, resulting in the value u, that is delivered to the given neuron. By its turn, the state or activation value of this neuron is calculated by the application of a threshold function to its input value, resulting in the final value v. This threshold function, also called activation function, frequently is non-linear, and must be chosen criteriously, as the performance of the neural network heavily depends on it. Generally this function is of the sigmoidal type.

Figure 1: Schematical representation of an artificial neuron.

How can a neural network "learn"? During the "training" step, real data - input and output - are continuously presented to it. Then it periodically compares real data with the results calculated by the neuron network. The difference between real and calculated results - that is, the error - is processed through a relatively complicated mathematical procedure, which adjusts the value of the synapse weights in order to minimize this error. This is an importante feature of the neural networks: their knowledge is stored in their synapse weights. The duration of the "training" step must be not excessively short, in order to allow the network to fully extract the relationships between variables. However, this step could not either be very long: in this case, the neural network will simply "memorize" the real data delivered to it, "forgetting" the relationships between them. So, it is advisable to break away approximately 20% of the available data in a subset and to use only the remaining 80% for the training of the neural network. The training step must be interrupted periodically and then the network must be tested using the 20% subset, checking the precision of the calculated results with real data. When the neural network precision stabilizes and stops to grow, it is time to consider the neural network as fully trained. There are two basic types of neural networks regarding data flow and training type. The Rummelhart type neural network shows data flow in one direction - that is, it is an unidirectional network. Its simplicity and stability makes it a natural choice for applications like data analysis, classification and interpolation. Consequentely, it is particularly suitable for process modeling, and, in fact, there is many real world applications of this type of network.

A fundamental characteristic of this network type is the arrangement of neurons in layers. Of course, there must have at least two layers in this kind of network: data input and data output. As the performance of two-layer neural networks is very limited, generally it is included at least one more intermediate layer, also called hidden layer. Each neuron is linked to all the neurons of the neighbouring layers, but there is no links between neurons of the same layer. The behavior of this kind of network is static; its output is a reflexion of its respective input. It must be previously trained using real data in order to perform adequately. The other neural network, of the Hopfield type, is characterized by a multidirectional data flow. Its behavior is dynamic and more complex than the Rummelhart networks. The Hopfield nets do not show neuron layers: there is total integration between input and output data, as all neurons are linked between themselves. These networks are tipically used for studies about optimization of connections like, for the example, the famous Travel Salesman Problem. This kind of neural network can be trained with or without supervision; the purpose of its training is the minimization of its energy, leading to an independent behavior. However, there is no practical application of this kind of network up to this moment.

As told before, applications particularly suited for neural networks are those which mathematical formulation is very hard or impossible. For example:

• Signal analysis and processing;
• Process control;
• Robotics;
• Data classification;
• Data smoothing;
• Pattern recognition;
• Image analysis;
• Speech analysis;
• Medical diagnostics;
• Stock market forecasting;
• Analysis for loan or credit solicitations;
• Oriented marketing.

The comparison between neural networks and expert systems shows that the development of the former technique is more quick, simple and cheap. However, a major drawback of the use of neural networks arises from the fact that it is not always possible to know how a neural network got a given result. Sometimes this can be very inconvenient, mainly when the neural network calculated results are atypical or unexpected. However, the use of hybrid artificial intelligent systems - that is, conjugated use of neural networks with expert systems or fuzzy logic - are increasingly showing good results, through the optimized use of its best characteristics.

There are some advantages of neural networks towards multiple regression. There is no need to select the most important independent variables in the data set, as neural networks can automatically select them. The synapses associated to irrelevant variables readily show negligible weight values; on its turn, relevant variables present significant synapse weight values. As said previously, there is also no need to propose a function as model, as required in multiple regression. The learning capability of neural networks allow them to "discover" more complex and subtle interactions between the independent variables, contributing to the development of a model with maximum precision. Besides that, neural networks are intrinsically robust, that is, they show more immunity to noise eventually present in real data; this is an important factor in the modelling of industrial processes. It must be noted that the criterious use of statistical techniques can be extremely useful in the preliminary analysis of raw data used for the development of a neural network. Data can be previously refined, minimizing even further the development time and effort of a reliable neural network, as well maximizing its precision. Hybrid statistical-neural networks systems can be a very useful solution to some specific problems.

There are countless examples of neural network applications in the metallurgy field. Some cases regarding hot rolling of steel are listed below:

• Sizing of slabs for plate rolling⁶;
• Modelling of hot strength of steel from temperature, strain and strain rate⁷;
• Same as above, including effect of chemical composition⁸;
• Determination of TTT diagrams from the chemical composition of steel⁹;
• Pass schedule calculation for hot strip mills^10,11.
• Feasibility of production of particular steel grades in a steelworks, evaluated from information about its required mechanical properties¹².

- BIBLIOGRAPHICAL REFERENCES

1. HECHT-NIELSEN, R. Neurocomputing. Addison-Wesley Publishing Company, Reading, 1990. 433 p.

2. EBERHART, R.C. & DOBBINS, R.W. (editors). Neural Network PC Tools - A Practical Guide. Academic Press, San Diego, 1990, 414 p.

3. MÜLLER, B. et al. Neural Networks: An Introduction. Springer-Verlag, Berlin, 1995, 330 p.

4. FREEMAN, J.A. & SKAPURA, D.M. Neural Networks: Algorithms, Applications and Programming Techniques. Addison-Wesley Publishing Company, Reading, 1992, 401 p.

5. BLUM, A. Neural Networks in C++. John Wiley & Sons, Inc., New York, 1992, 214 p.

6. OLIVEIRA, J.B. et al. "Use of Neural Networks in the Plate Production Scheduling at USIMINAS". In: Seminário de Laminação, Associação Brasileira de Metais, Porto Alegre, 1992, 319-339.

7. GORNI, A.A. "Mathematical Modeling of the Hot Strength of HSLA Steels". In: 1st Metal Forming Week, Associação Brasileira de Metalurgia e Materiais, Joinville, 1993, 267-86

8. LENARD, J.G. et al. "A Comparative Study of Artificial Neural Networks for the Prediction of HSLA and Carbon Steels". Steel Research, February 1996, 59-65

9. DOUNADILLE, C. et al. "Usage de Reseaux Neuronaux por Prevision des Courbes de Transformations de Acier". Revue de Metallurgie - CIT, Oct. 1992, 892-94.

10. ORTMANN, B. et al. "Modernization of the Automation in the Hot Wide Strip Mill at Voest-Alpine Stahl". Metallurgical Plant and Technology - International, 6/1994, 26-34.

11. PORTMANN, N. et al. "Application of Neural Networks in Rolling Mill Automation". Iron and Steel Engineer, Feb. 1995, 33-6

12. WATANABE, M. et al. "Development of Shape Steel Quality Design Expert System". Nippon Steel Technical Report, April 1992, 29-44.

	Last Update: 27 November 1997
	© Antonio Augusto Gorni